通常の場合は「-」(ハイフン)の記号で引き算をしますが、MINUS関数を使う例も考えられます。また、「いくつかの数値の合計をまとめて差し引く」場合や「次々引いていく」といった計算で関数を用いる例も紹介します。
「-」記号やMINUS関数で引き算する例
通常の単純な引き算の例です。
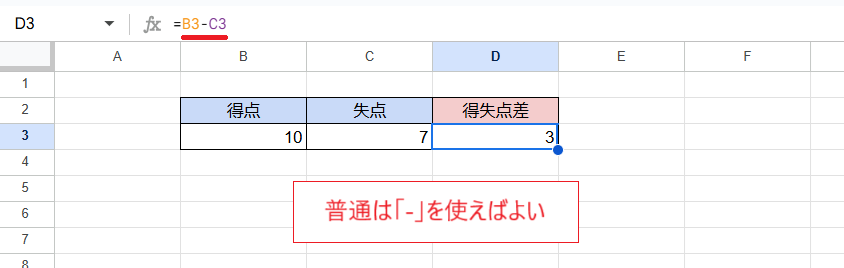
次の画像ではD3セルに「=B3-C3」と入力して2つのセルの数値の差を求めています。
このように、2つの数値の間に「-」の記号(ハイフン)を入れれば引き算を行うことができます。
ところでGoogleスプレッドシートにはMINUS関数というものも用意されています。
次の画像では「=MINUS(B3,C3)」と入力して2つのセルの数値の差を求めています。もちろん結果は1つ上の画像と同じ「3」となります。
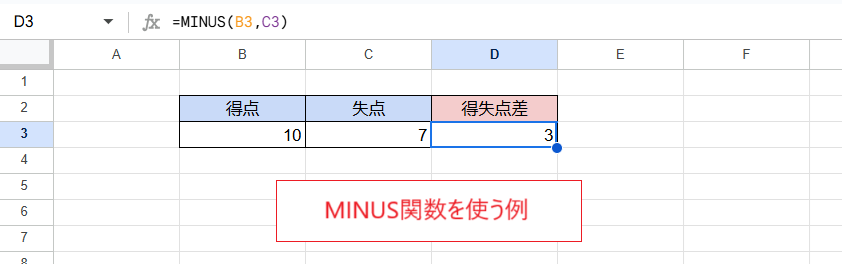
このMINUS関数はExcelにはない関数で、第1引数から第2引数の値を差し引く、つまり引き算をします。
しかし特殊な機能はなく、あえてメリットを挙げるとすれば「ハイフンを使わずに引き算ができる」ということぐらいですので、あまり深く考えず「-」を使った方がよいでしょう。
なお、Googleスプレッドシートでは同様に足し算のADD関数、掛け算のMULTIPLY関数、割り算のDIVIDE関数というものが用意されています。いずれも2つしか引数を指定できず、やはり「+」「*」「/」を使った方が簡単です(SUM関数、PRODUCT関数、QUOTIENT関数とは異なる関数ですので注意してください)。
まとめて差し引く例
上記のように引き算は「-」記号で済むのですが、実際に引き算の際に関数を使うとすれば「いくつかの数値をまとめて差し引く」というケースが考えられます。
次の画像ではC8セルに数式を入力し、C2セルの値からC4~C7セルの値をまとめて差し引いた結果を得ています(1000-140-210-180-170=300)。
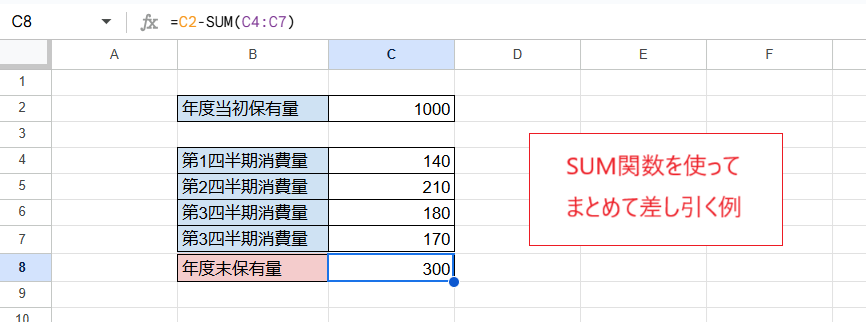
C8セル
=C2-SUM(C4:C7)
「SUM(C4:C7)」でC4~C7セルの値の合計を求めて、「-」を使いC2セルの値から差し引いています。
「=SUM(C2,-C4:C7)」で同じ計算ができればスマートな感じはしますがこれではダメで、「=SUM(C2,ARRAYFORMULA(-C4:C7))」のようにする必要があります。
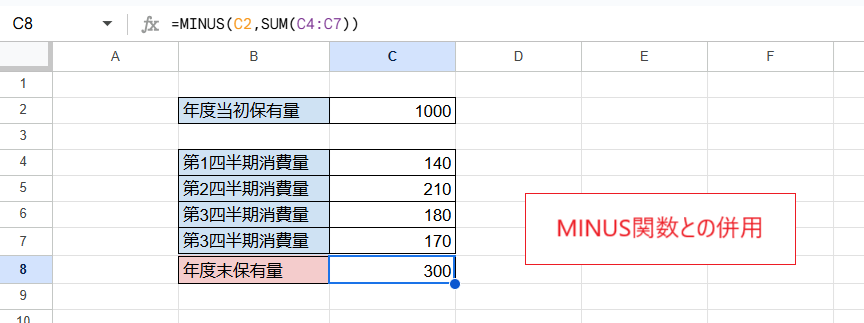
次の画像ではあえてMINUS関数を使い「=MINUS(C2,SUM(C4:C7))」とし、1つ上の画像と同じ計算をしています。
「=SUM(C2,ARRAYFORMULA(-C4:C7))」よりはマシに思われますが、やはり実用的とはいえません。
次々引いていく計算の例
ある数値から、いくつかの数値をどんどん引いていくという累計計算の一種です。関数を使わない例も考えられますがここではSUM関数と絶対参照($)を使う例とSCAN/LAMBDA関数を使う例の2つの例を紹介します。
次の画像ではC2セルの値からC5~C8の値を次々引いた結果を得ています。
具体的にはD5セルに数式を入力し、D8セルまでフィルコピー(セル右下の青い丸をダブルクリックするか下方にドラッグ)しています。
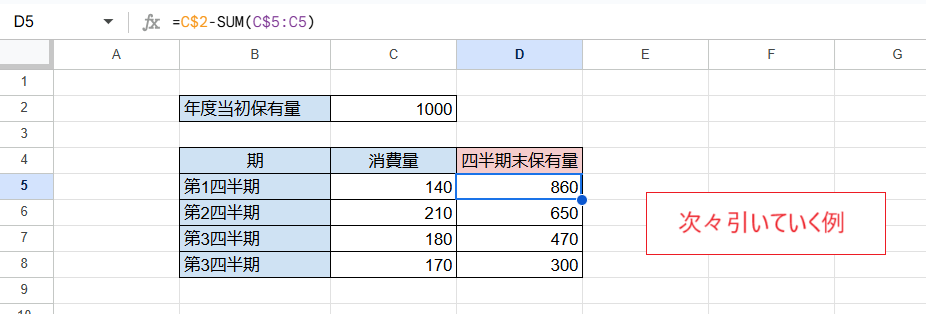
D5セル(D8セルまでフィルコピー)
=C$2-SUM(C$5:C5)
C2セルの値からC5:C5の範囲(つまりC5セルの値)を引いた結果を求めています。
ここだけ見ると「=C2-C5」と同じですが、フィルコピーに伴い各セルでSUM関数に含まれる範囲が変化していくのがポイントです。
ここでD6セルを選択してみると数式は「=C$2-SUM(C$5:C6)」となっており、C2セルの値からC5,C6の2つの数値を引いた結果が得られていることがわかります。
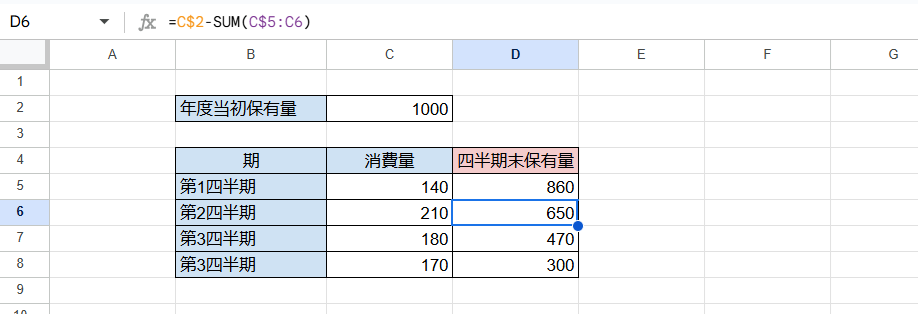
同様にC7セルでは「=C$2-SUM(C$5:C7)」となり3つの数値を引いた結果が、C8セルでは「=C$2-SUM(C$5:C8)」となり4つの数値を引いた結果が得られています。絶対参照($)が付いている部分はコピーに伴い変化しないことに注意してください。
次の画像はもう1つのやり方の例です。
ここではD5セルに1つの数式を入力するだけで同じ結果(D5~D8セル)を得ています。
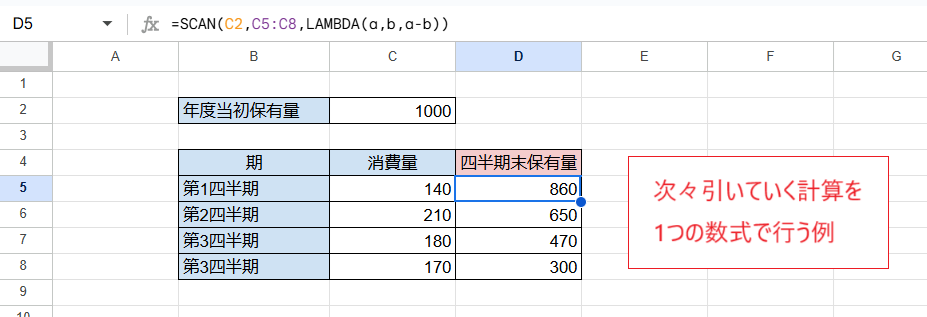
D5セル
=SCAN(C2,C5:C8,LAMBDA(a,b,a-b))
SCAN関数を使うことで引き算を繰り返し、1回ごとに結果を表示させています。
もう少し説明すると、C2セルの値にaと、C5:C8セルの範囲にbと名付け、aからbの各要素(C5セル~C8セル)の値を次々引いていき、都度結果を表示させています。
ちょっと難しい関数ですが、計算(ここでは引き算)した結果に対してさらに計算を繰り返すことができるのがポイントです。