いきなり答える備忘録

Google Workspace・Microsoft 365・LibreOfficeなどに関するメモ

（Excel）一般化した金種計算の例

Excel

　Excelで、貨幣の種類がどのようなものであっても1つの同じ式で金種計算を行う計算の例です。
　式が複雑になり、決して実用的とは言えませんが参考まで。

  • REDUCE/LAMBDA関数を活用して、どのような金種にも対応できる金種計算を行うことができます。

手順

　B3:B11の範囲には金種計算の対象となる金額（合計金額）を、C2:L2の範囲には2,000円を含む日本のすべての種類の金種（貨幣）を入力しています（左の金種ほど高額になるようにソートされている必要があります）。
　これに対しC3セルに式を入力して、各金種の必要枚数を出力させています。
　2,000円を考慮した金種計算は少々厄介なものになりますが、正しく計算できているのがわかります。

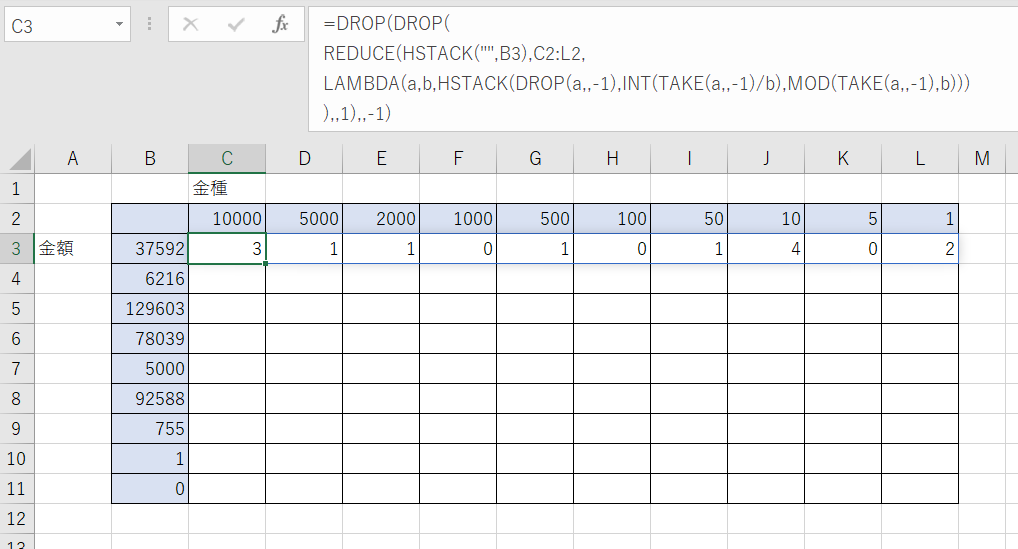
　C3セル

=DROP(DROP(
REDUCE(HSTACK("",B3),C2:L2,
LAMBDA(a,b,HSTACK(DROP(a,,-1),INT(TAKE(a,,-1)/b),MOD(TAKE(a,,-1),b)))
),,1),,-1)

　基本的には金額を10000で割った商（小数切捨。以下同様）を求め、その余りを5000で割った商を求め……ということを繰り返しています。
　具体的な式の内容ですが、REDUCE関数とLAMBDA関数を使い、「HSTACK("",B3)」をa（の初期配列）、「C2:L2」をbと名付けています。
　bのそれぞれの値について、「aの最後のセルを削除し、『aの最後のセルにあった値をbで割った商』のセルを追加し、さらに『aの最後のセルにあった値をbで割った余り』のセルを追加する」という操作を繰り返しています。
　具体的に37592という金額に対して配列aは次のように変化していきます。

　{"",37592}
　{"",3,7592}
　{"",3,1,2592}
　{"",3,1,1,592}
　{"",3,1,1,0,592}
　・
　・
　{"",3,1,1,0,1,0,1,4,0,2,0}

　最初の空白セル（初回のDROPでエラーにならないためのセル）と最後の0（「1」の貨幣に対する余り）は結果から除く必要がありますので、二重のDROP関数で削除して完了となります。
　REDUCE関数内だけみれば案外複雑でもないのですが、それでも到底スマートとはいえないのが痛いところです。


　なお、対象となる金額である「B3」を「B3:B11」に変更するだけで、すべての金額に対する金種計算ができます。

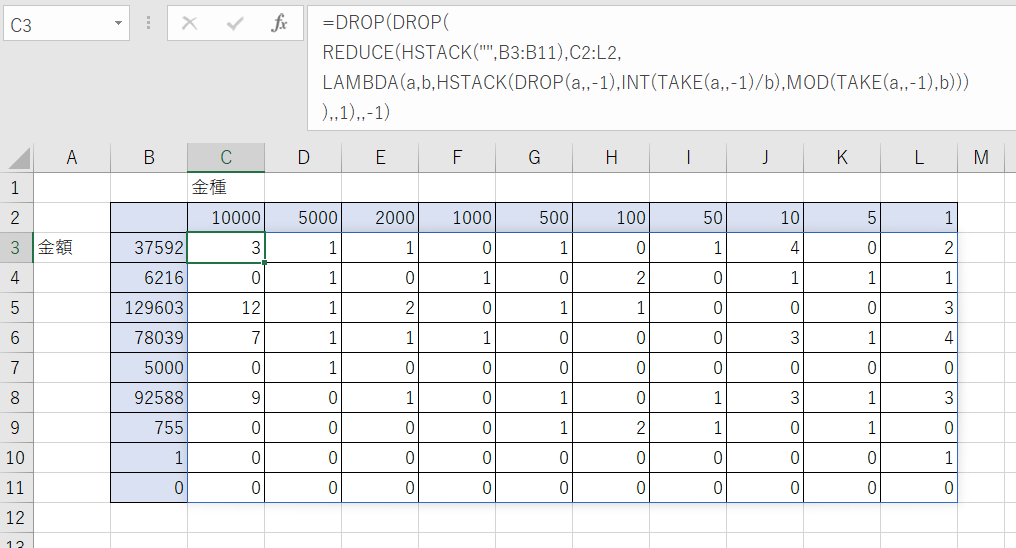
　C3セル

=DROP(DROP(
REDUCE(HSTACK("",B3:B11),C2:L2,
LAMBDA(a,b,HSTACK(DROP(a,,-1),INT(TAKE(a,,-1)/b),MOD(TAKE(a,,-1),b)))
),,1),,-1)

　「C2:L2」に対する絶対参照を行う必要はなく、まさにスピルのメリットといえます。


　さらに金種の内容を変更した結果です。
　このように、どれほど珍妙な通貨体系であっても正しく計算されます（もちろん、金種の数が増減した場合は参照範囲を変更する必要があります）。

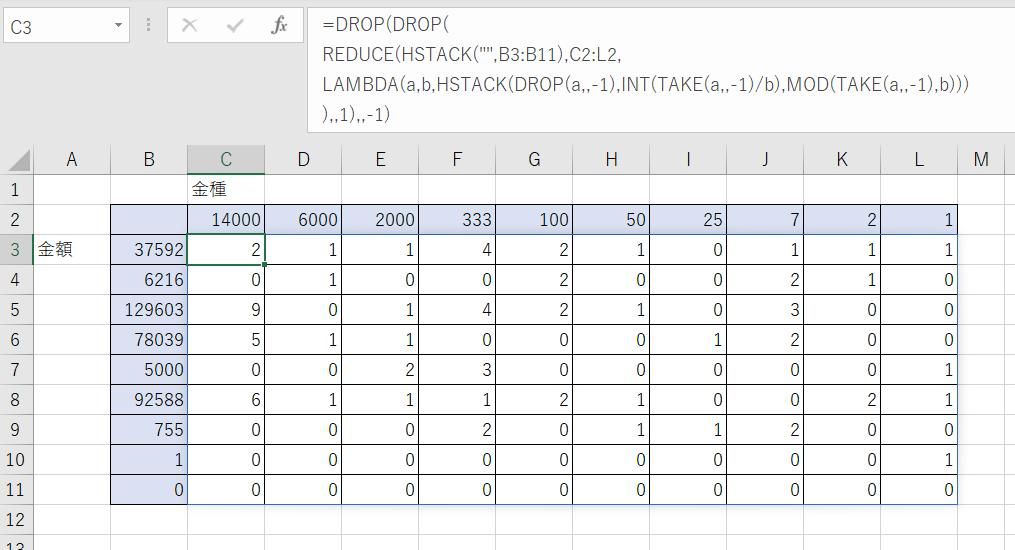
　最後に備考ですが、解が存在しないケース（「1」の貨幣が存在しない場合に起こります）では、金種計算の結果と金額が一致しない結果になります。もし現実に「1」の貨幣が存在しない場合、それでも金種欄には「1」の貨幣を設け、その必要枚数が0でなければ解が存在しないとみなすのがよいでしょう。

accs2014