なお、ここでのナップザック問題とは1種のアイテムについて1個選択するかしないかという選択肢しかない、0-1ナップザック問題です。
- 各種関数を組み合わせることでナップザック問題を解くことができます。
手順
B,C列にアイテムの価値と重量の組み合わせを記録しています。C2にはアイテム数を、C3には上限重量を記録しています。
このあたりのデータの持ち方も式の内容に影響してきますが、いずれF4セルに式を入力し、上限重量を超えない範囲で合計価値が大きい順(左→右)にアイテムの組み合わせを表示させています。
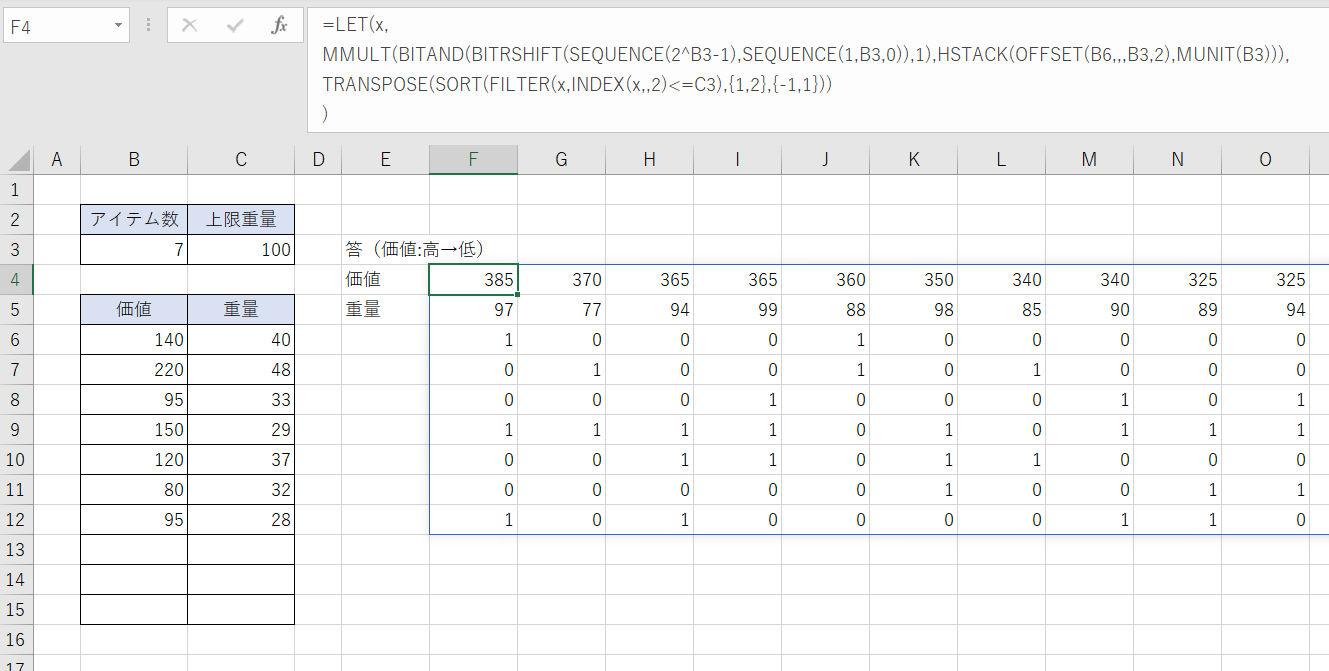
合計価値の最大値は385で、その時の重量は97、アイテムの組み合わせは上から1,4,7番目のものとなります(F4:F12に表示されている結果)。
合計価値が2番目に大きい結果についてはG4:G12に、3番目はさらにその右に……と表示されています。合計価値が同じ値になる場合は重量が小さい組み合わせが左に表示されるようになっています。
式の内容は次の通りです。
F4セル
=LET(x,
MMULT(BITAND(BITRSHIFT(SEQUENCE(2^B3-1),SEQUENCE(1,B3,0)),1),HSTACK(OFFSET(B6,,,B3,2),MUNIT(B3))),
TRANSPOSE(SORT(FILTER(x,INDEX(x,,2)<=C3),{1,2},{-1,1}))
) まず「SEQUENCE(2^B3-1)」により1から2^B3-1(ここでは2^7-1=127)までの値を生成し、BITRSHIFT/BITAND関数と併用することで{1,0,0,0,0,0,0}から{1,1,1,1,1,1,1}までの配列、つまりアイテム選択の全組み合わせを表す行列を生成しています。
「HSTACK(OFFSET(B6,,,B3,2),MUNIT(B3))」により各アイテムの価値(1行7列)、重量(1行7列)、7×7の単位行列を横に並べた行列を生成しています。
そしてMMULT関数により2つの行列の積算を行っています。これで全組み合わせについての合計価値、合計重量、アイテム選択の内容が得られます。これをLET関数でxと名付けています。
最後にFILTER関数を使い合計重量が上限重量を越えている組み合わせを削除し、SORT関数により合計価値の降順、合計重量の昇順でソートし、TRANSPORT関数により左の表に合わせるように(アイテム選択の内容がわかりやすいように)転置して表示させています。
参考までにMMULT関数内の第1項(アイテム選択の全組み合わせを表す行列)だけを実行すると次のような結果になります。
最初の行が{1,0,0,0,0,0,0}、最後の行が{1,1,1,1,1,1,1}である127行の行列が生成されています。
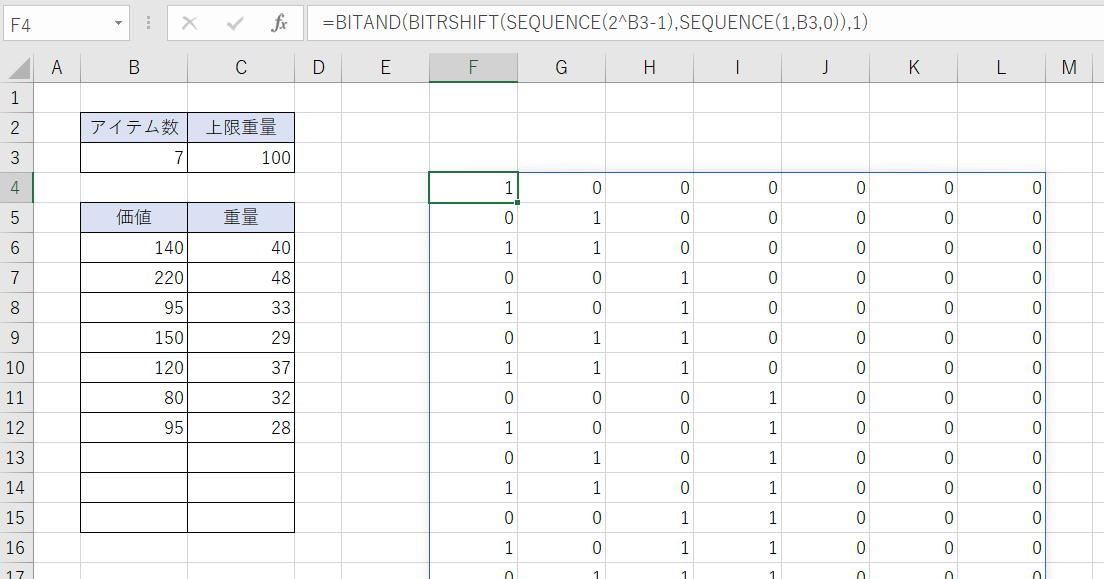
F4セル
=BITAND(BITRSHIFT(SEQUENCE(2^B3-1),SEQUENCE(1,B3,0)),1)
この部分に関しては1から2^B3-1をBASE関数などで2進数にして分割するという方法もありますが、今回はBITANDを使ったプログラミングっぽいアプローチにしています。
また、MMULT関数内の第2項だけを実行すると次のような結果になります。
上記の説明の繰り返しになりますが、左の表内に入力されている各アイテムの価値、重量と単位行列を横に並べただけです。
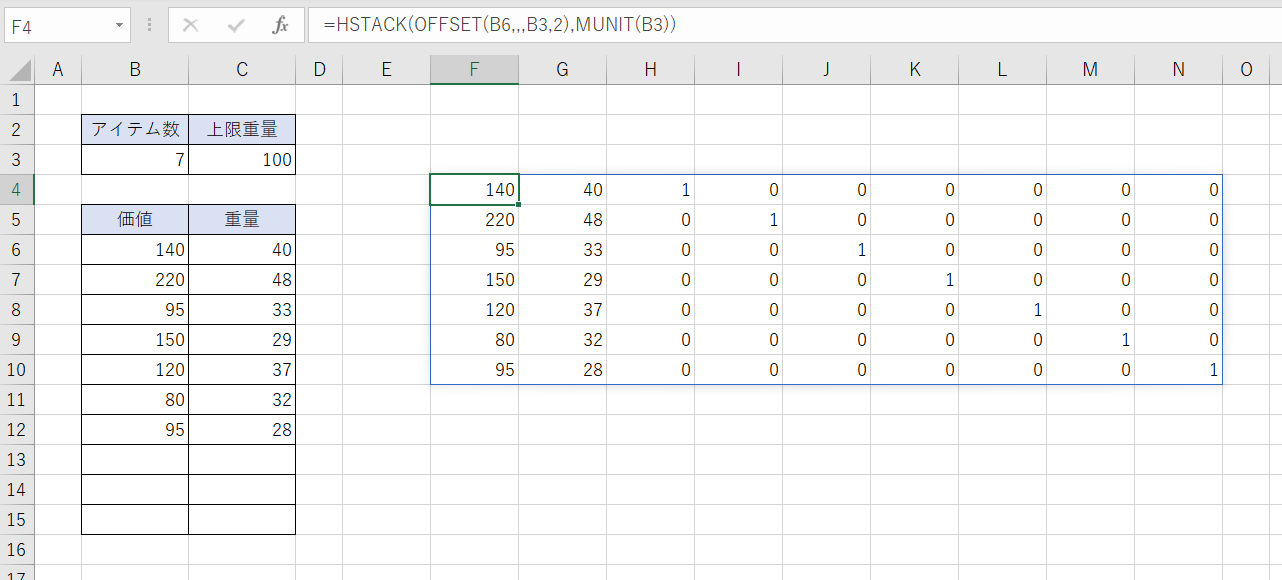
F4セル
=HSTACK(OFFSET(B6,,,B3,2),MUNIT(B3))
MMULT関数の結果(x)を表示すると次のようになります。
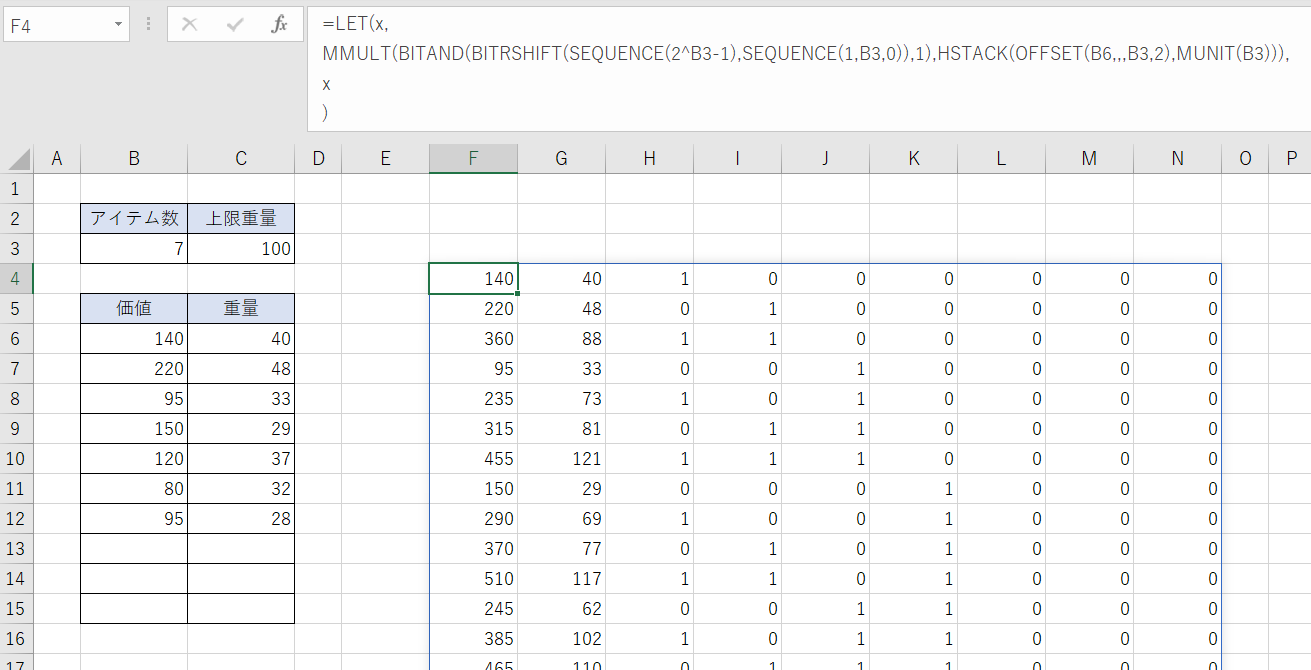
F4セル
=LET(x, MMULT(BITAND(BITRSHIFT(SEQUENCE(2^B3-1),SEQUENCE(1,B3,0)),1),HSTACK(OFFSET(B6,,,B3,2),MUNIT(B3))), x )
必要とする結果はこの段階ですべて得られています。
これにフィルタとソートをかけて転置した結果が最初の画像です。
最後に補足ですが、総当たりですのでアイテムが増えると急激に重くなります。
また、通常全部の組み合わせは要らないと思いますので、さらにTAKE関数を使って必要な数だけに絞るのがよいでしょう。